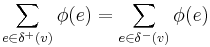Nowhere-zero flow

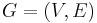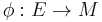In graph theory, nowhere-zero flows are a special type of network flow which is related (by duality) to coloring planar graphs. Let $G = (V,E)$ be a directed graph and let $M$ be an abelian group. 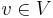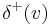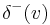We say that a map $\phi�: E \rightarrow M$ is a flow or an M-flow if the following condition (sometimes called the Kirchoff Rule) is satisfied at every vertex $v \in V$ (here we let $\delta^%2B(v)$ denote the set of edges pointing away from $v$ and $\delta^-(v)$ the set of edges pointing toward $v$ ).

$\sum_{e \in \delta^%2B(v)} \phi(e) = \sum_{e \in \delta^-(v)} \phi(e)$

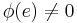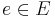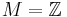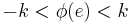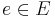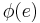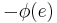If $\phi(e) \neq 0$ for every $e \in E$ , we call $\phi$ a nowhere-zero flow. If $M = {\mathbb Z}$ and $k$ is a positive integer with the property that $-k < \phi(e) <k$ for every edge $e$ , we say that $\phi$ is a $k$ -flow. Consider a flow $\phi$ on $G$ and modify it by choosing an edge $e \in E$ , reversing it, and then replacing $\phi(e)$ with $-\phi(e)$ . After this adjustment, $\phi$ is still a flow, and further this adjustment preserves the properties $k$ -flow and nowhere-zero flow. Thus, the existence of a nowhere-zero $M$ -flow and the existence of a nowhere-zero $k$ -flow is independent of the orientation of the graph, and we will say that an (undirected) graph has a nowhere-zero $M$ -flow or k-flow if some (and thus every) orientation of it has such a flow.

Flow/coloring duality

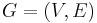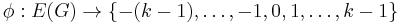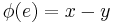Let $G=(V,E)$ be a directed bridgeless graph drawn in the plane, and assume that the regions of this drawing are properly $k$ -colored with the colors {0, 1, 2, .., k − 1}. Now, construct a map $\phi:E(G)\rightarrow\{-(k-1),\dots,-1,0,1,\dots,k-1\}$ by the following rule: if the edge $e$ has a region of color $x$ to the left and a region of color $y$ to the right, then let $\phi(e)=x-y$ . It is an easy exercise to show that $\phi$ is a $k$ -flow. Furthermore, since the regions were properly colored, $\phi$ is a nowhere-zero $k$ -flow. 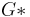It follows from this construction, that if $G$ and $G*$ are planar dual graphs and 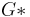$G*$ is $k$ -colorable, then $G$ has a nowhere-zero $k$ -flow. Tutte proved that the converse of this statement is also true. Thus, for planar graphs, nowhere-zero flows are dual to colorings. Since nowhere-zero flows make sense for general graphs (not just graphs drawn in the plane), this study can be viewed as an extension of coloring theory for non-planar graphs.

Theory

Unsolved problems in mathematics
Does every bridgeless graph have a nowhere zero 5-flow? Does every bridgeless graph that does not have the Petersen graph as a minor have a nowhere zero 4-flow?

Just as no graph with a loop edge has a proper coloring, no graph with a bridge can have a nowhere-zero flow (in any group). It is easy to show that every graph without a bridge has a nowhere-zero 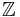${\mathbb Z}$ -flow (a form of Robbins theorem), but interesting questions arise when we try to find nowhere-zero $k$ -flows for small values of $k$ . Two nice theorems in this direction are Jaeger's 4-flow theorem (every 4-edge-connected graph has a nowhere-zero 4-flow)^[1] and Seymour's 6-flow theorem (every bridgeless graph has a nowhere-zero 6-flow).^[2]

W. T. Tutte conjectured that every bridgeless graph has a nowhere-zero 5-flow^[3] and that every bridgeless graph that does not have the Petersen graph as a minor has a nowhere-zero 4-flow.^[4] For cubic graphs with no Petersen minor, a 4-flow is known to exist as a consequence of the snark theorem but for arbitrary graphs these conjectures remain open.

References

^ F. Jaeger, Flows and generalized coloring theorems in graphs, J. Comb. Theory Set. B, 26 (1979), 205-216.
^ P. D. Seymour, Nowhere-zero 6-flows, J. Comb. Theory Ser B, 30 (1981), 130-135.
^ 5-flow conjecture, Open Problem Garden.
^ 4-flow conjecture, Open Problem Garden.

T.R. Jensen and B. Toft, Graph Coloring Problems, Wiley-Interscience Serires in Discrete Mathematics and Optimization, (1995)